

It may be the case, that one particular method of presentation may be more conducive to solving a specific problem than another method. There are several different formats for presenting proofs. Write your proof so that someone that is not familiar with the problem will easily understand what you are saying.
Geometry proofs list how to#
Each statement in your proof must be clearly presented and supported by a definition, postulate, theorem or property. Introduction In this section, you will learn how to graph conic sections.
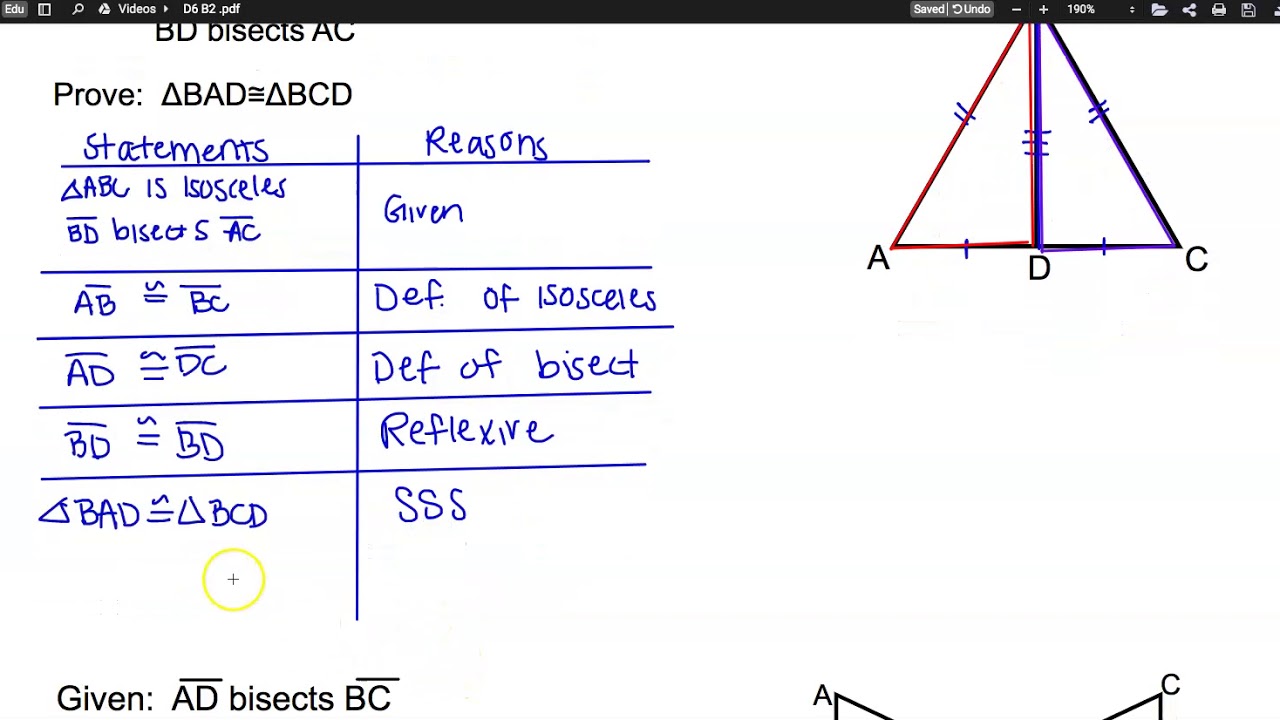
The argument may use other previously established statements, such as theorems but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Like in a game of chess, you must plan ahead so you will know which moves will lead to your victory of proving the statement true. A mathematical proof is a deductive argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. As such, it is important to maintain a chronological order to your presentation of the proof. The steps in a proof are built one upon the other. (Hope it helped) Find more proofs and geometry content at If you have questions, suggestions, or requests, let us know. PRACTICE EXERCISES - SOLUTIONS - Thanks for visiting. Direct proofs apply what is called deductive reasoning: the reasoning from proven facts using logically valid steps to arrive at a conclusion. Topics include triangle characteristics, quadrilaterals, circles, midpoints, SAS, and more. The most common form of proof is a direct proof, where the "prove" is shown to be true directly as a result of other geometrical statements and situations that are true.


 0 kommentar(er)
0 kommentar(er)
